Definisi turunan bisa dijelaskan sebagi berikut misalkan ada y yang merupakan fungssi dari x, ditulis y = f(x). Yang dimaksud dengan turun y terhadap x (dinotasikan dy/dx) atau sering ditulis y’ (baca : “y aksen”) didefinisikan sebagai
Rumus – Rumus Turunan Fungsi Matematika
Rumus 1 : Jika y = cxn dengan c dan n konstanta real , maka dy/dx = cn xn-1
contoh
y = 2x4
y = 2x4
dy/dx = 4.2x4-1 = 8x3
Rumus 2 : Jika y = c dengan c adalah konstanta maka dy/dx = 0
contoh:
contoh:
y = 6
y’= 0
Rumus 3 : Jika y = f(x) + g(x) maka turunannya sama dengan turunan dari masing-masing fungsi = f'(x) + g'(x)
contoh:
y = x3 + 2x2
contoh:
y = x3 + 2x2
y’ = 3x2 + 4x
Rumus 4 : Turunan Perkalian Fungsi Jika y f(x).g(x) maka y’ = f'(x) . g(x) + g'(x) . f(x)
contoh:
y = x2 (x2+2) maka,
f(x) = x2
f'(x) = 2x
g(x) = x2+2
g'(x) = 2x
kita masukkan ke rumus y’ = f'(x) . g(x) + g'(x) . f(x)
y’ = 2x (x2+2) + 2x . x2
y’ = 4x3 + 4x
Rumus 5 : Turunan Pembagian Fungsi
contoh:
y = x2 (x2+2) maka,
f(x) = x2
f'(x) = 2x
g(x) = x2+2
g'(x) = 2x
kita masukkan ke rumus y’ = f'(x) . g(x) + g'(x) . f(x)
y’ = 2x (x2+2) + 2x . x2
y’ = 4x3 + 4x
Rumus 5 : Turunan Pembagian Fungsi
Rumus 6 : jika sobat punya y = [f(x)]n maka turunannya adalah n [f(x)]n-1 . f'(x)
contoh:
Rumus 7 : Turunan Logaritma Natural misal y = ln f(x) maka turunannya
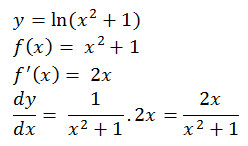
Rumus 8 : ef(x) maka dy/dx = ef(x).f'(x)
contoh :
y = e2x+1
f(x) = 2x+1
f'(x) = 2
maka f’ = e2x+1 . 2 = 2e2x+1
Rumus 9 : Turunan Trigonometri Sin
misal:
y = sin f(x) maka y’ = cos f(x) . f'(x)
contoh :
y = sin(x2 + 1)
y’ = cos (x2 +1) . 2x = 2x. cos (x2 +1)
contoh :
y = sin(x2 + 1)
y’ = cos (x2 +1) . 2x = 2x. cos (x2 +1)
Rumus 10 : Turunan Trigonometri Cos
misal:
y = cos f(x) maka y’ = -sin f(x). f'(x)
contoh :
y = cos (2x+1)
y’ = -sin (2x+1) . 2 = -2 sin (2x+1)
contoh :
y = cos (2x+1)
y’ = -sin (2x+1) . 2 = -2 sin (2x+1)

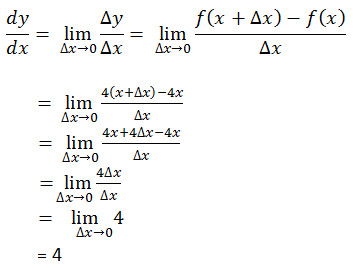

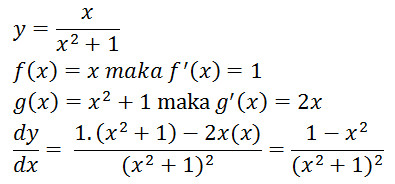
![y= √(x^2+1) f(x)=x^2+1 dan f^' (x)=2x y= √(x^2+1)=〖〖(x〗^2+1)〗^(1/2) dy/dx= 1/2 [x^2+1]^(1/2-1) (2x)=x[x^2+1]^(-1/2) =x/√(x^2+1)](http://rumushitung.com/wp-content/uploads/2014/01/turunan-pangkat.jpg)

No comments:
Post a Comment